How to Convert Gray Code To Binary? Solve using K-map.

Conversion of Gray Code to Binary using K-map method.

Finding Truth table and expressions for K-map.

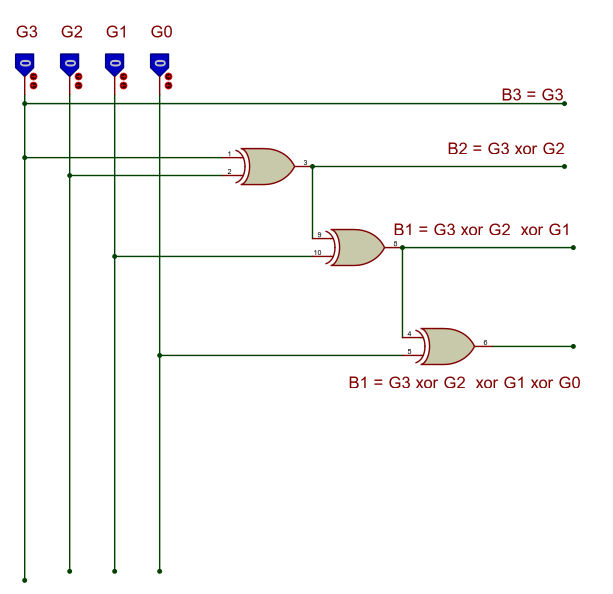
Implementation using logic gates.

Truth Table -

To find truth table first it is neccessary to know about gray code and binary code then it can be found easily.

I have made truth table for your simplicity.

How To Solve -

Now, To solve it we need truth table which i have already made.

Lets consider first for output B₃ , see column B₃ and find the rows where B₃ is 1 and notedown corresponding input values.

Now, for this corresponding value write decimal value.

Now, once you got all of these things you are ready for writing your first expression -

write it as , B₃ = Σ_m( 8, 9, 10, 11, 12, 13, 14, 15 )

Similarly take output B₂ and find 1's in the column and for input find corresponding decimal value and write it.

Output Expression For K-map -

B₃ = Σ_m( 8, 9, 10, 11, 12, 13, 14, 15 )

B₂ = Σ_m( 4, 5, 6, 7, 12, 13, 14, 15 )

B₁ = Σ_m( 2, 3, 4, 5, 8, 9, 14, 15 )

B₀ = Σ_m( 1, 2, 4, 7, 8, 11, 13, 14)

K-map for B3 -

B₃ = Σ_m( 8, 9, 10, 11, 12, 13, 14, 15 )

B₃= G₃

K-map for B2 -

B₂ = Σ_m( 4, 5, 6, 7, 8, 9, 10, 11 )

B₂= G₃'G₂ +G₃G₂'

K-map for B1 -

B₁ = Σ_m( 2, 3, 4, 5, 8, 9, 14, 15 )

B₁= G₃G₂'G₁' + G₃'G₂G₁' + G₃'G₂'G₁ + G₃G₂G₁

K-map for B0 -

B₀ = Σ_m( 1, 2, 4, 7, 8, 11, 13, 14)

B₀= G₀G₁'G₂'G₃' + G₀'G₁G₂'G₃' + G₀'G₁'G₂G₃' + G₀G₁G₂G₃' + G₀G₁'G₂G₃ + G₀'G₁G₂G₃ + G₀G₁G₂'G₃ + G₀G₁'G₂'G₃

Output Boolean Expression -

B₃= G₃

B₂= G₃'G₂ +G₃G₂' = G₃⊕ G₂

B₁= G₃G₂'G₁' + G₃'G₂G₁' + G₃'G₂'G₁ + G₃G₂G₁

= G₁' ( G₃G₂’ + G₃’G₂) + G₁( G₃’G₂’ + G₃G₂)

= G₁' ( G₃⊕ G₂) + G₁( G₃⊕ G₂)'

= G₃⊕ G₂⊕ G₁

B₀= G₀G₁'G₂'G₃' + G₀'G₁G₂'G₃' + G₀'G₁'G₂G₃' + G₀G₁G₂G₃' + G₀G₁'G₂G₃ + G₀'G₁G₂G₃ + G₀G₁G₂'G₃ + G₀G₁'G₂'G₃

= G₂'G₃' ( G₀G₁' + G₀'G₁)+ G₂G₃' (G₀'G₁' + G₀G₁) + G₂G₃ ( G₀G₁' + G₀'G₁)+ G₂'G₃ (G₀'G₁' + G₀G₁)

= G₂'G₃' ( G₀ ⊕ G₁)+ G₂G₃' ( G₀ ⊕ G₁)' + G₂G₃ ( G₀ ⊕ G₁)+ G₂'G₃ ( G₀ ⊕ G₁)'

= ( G₀ ⊕ G₁) [G₂'G₃' + G₂G₃ ] + ( G₀ ⊕ G₁)' [ G₂G₃' + G₂'G₃ )

= ( G₀ ⊕ G₁) ( G₂ ⊕ G₃ )' + ( G₀ ⊕ G₁)' ( G₂ ⊕ G₃ )

= G₃⊕ G₂⊕ G₁⊕ G₀