- Published on
How to Convert Gray Code To Binary? Solve using K-map.
- Authors
- Name
- admin
Conversion of Gray Code to Binary using K-map method.
Finding Truth table and expressions for K-map.
Implementation using logic gates.
Truth Table -
To find truth table first it is neccessary to know about gray code and binary code then it can be found easily.
I have made truth table for your simplicity.
How To Solve -
Now, To solve it we need truth table which i have already made.
Lets consider first for output B3 , see column B3 and find the rows where B3 is 1 and notedown corresponding input values.
Now, for this corresponding value write decimal value.
Now, once you got all of these things you are ready for writing your first expression -
write it as , B3 = Σm( 8, 9, 10, 11, 12, 13, 14, 15 )
Similarly take output B2 and find 1's in the column and for input find corresponding decimal value and write it.
Output Expression For K-map -
B3 = Σm( 8, 9, 10, 11, 12, 13, 14, 15 )
B2 = Σm( 4, 5, 6, 7, 12, 13, 14, 15 )
B1 = Σm( 2, 3, 4, 5, 8, 9, 14, 15 )
B0 = Σm( 1, 2, 4, 7, 8, 11, 13, 14)
K-map for B3 -
B3 = Σm( 8, 9, 10, 11, 12, 13, 14, 15 )
B3 = G3
K-map for B2 -
B2 = Σm( 4, 5, 6, 7, 8, 9, 10, 11 )
B2 = G3'G2 +G3G2'
K-map for B1 -
B1 = Σm( 2, 3, 4, 5, 8, 9, 14, 15 )
B1 = G3G2'G1' + G3'G2G1' + G3'G2'G1 + G3G2G1
K-map for B0 -
B0 = Σm( 1, 2, 4, 7, 8, 11, 13, 14)
B0 = G0G1'G2'G3' + G0'G1G2'G3' + G0'G1'G2G3' + G0G1G2G3' + G0G1'G2G3 + G0'G1G2G3 + G0G1G2'G3 + G0G1'G2'G3
Output Boolean Expression -
B3 = G3
B2 = G3'G2 +G3G2' = G3 ⊕ G2
B1 = G3G2'G1' + G3'G2G1' + G3'G2'G1 + G3G2G1
= G1' ( G3G2’ + G3’G2 ) + G1 ( G3’G2’ + G3G2 )
= G1' ( G3 ⊕ G2 ) + G1 ( G3 ⊕ G2 )'
= G3 ⊕ G2 ⊕ G1
B0 = G0G1'G2'G3' + G0'G1G2'G3' + G0'G1'G2G3' + G0G1G2G3' + G0G1'G2G3 + G0'G1G2G3 + G0G1G2'G3 + G0G1'G2'G3
= G2'G3' ( G0G1' + G0'G1 ) + G2G3' (G0'G1' + G0G1 ) + G2G3 ( G0G1' + G0'G1 ) + G2'G3 (G0'G1' + G0G1 )
= G2'G3' ( G0 ⊕ G1 ) + G2G3' ( G0 ⊕ G1 )' + G2G3 ( G0 ⊕ G1 ) + G2'G3 ( G0 ⊕ G1 )'
= ( G0 ⊕ G1 ) [ G2'G3' + G2G3 ] + ( G0 ⊕ G1 )' [ G2G3' + G2'G3 )
= ( G0 ⊕ G1 ) ( G2 ⊕ G3 )' + ( G0 ⊕ G1 )' ( G2 ⊕ G3 )
= G3 ⊕ G2 ⊕ G1 ⊕ G0
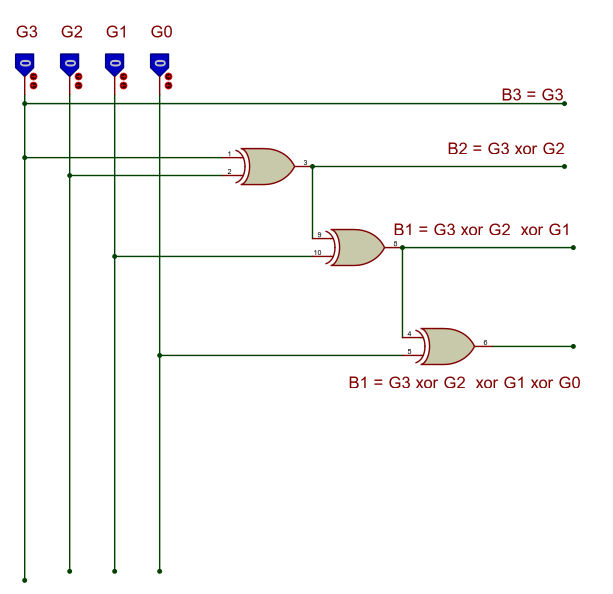
Implementation using Basic Gates -