How to make adder circuit using multiplexer and decoder

Designing adder circuit using multiplexers and also from decoders.

Full Adder Demonstration.

Full adder using logic gates.

 

Full Adder Introduction -

Full Adder is logic of addition in which two numbers are added along with carry input. It means there will be three input in which one is carry input. It will help when we have a carry from some another logics or from any previous addition.

 

Full Adder Truth Table -

A

B

Cin

S

Cout

0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Full Adder K-map Solutions -

K-map Expression for outputs from truth table -

 Sum ,       S ( A, B, C_in ) = ∑_m ( 1, 2, 4, 7 ) 

 Carry ,  C_out ( A, B, C_in ) = ∑_m ( 3, 5, 6, 7 ) 

•  K-map for S -

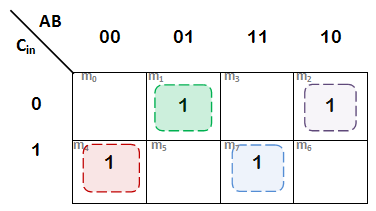
From K-map, S = A'BC' + AB'C' + A'B'C + ABC

•  K-map for C_out -

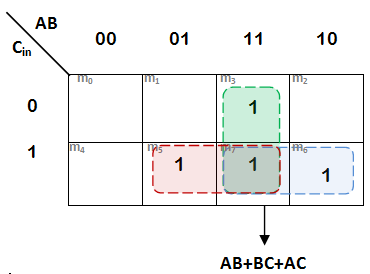
From K-map, C_out = AB + BC + AC

K-map Solutions -

S   = A'BC' + AB'C' + A'B'C + ABC

or   = C'( A'B + AB' ) + C( A'B' + AB ) 

or   = C'( A ⊕ B ) + C( A ⊕  B ) '

 S   =  A ⊕ B ⊕ C 

 

 C_out = AB + BC + AC 

or      = ABC' + A'BC + AB'C + ABC

or      = ABC' + ( A'B + AB' ) C + ABC

or      = AB( C' + C ) + ( A'B + AB' ) C 

C_out      = AB + ( A ⊕ B ) C 

Implementation using basic gates -

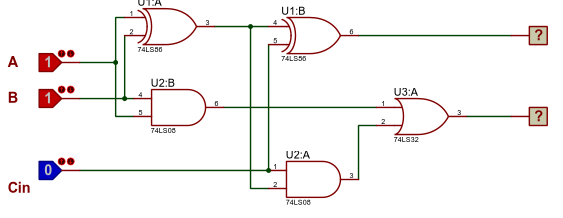
Implementation using Multiplexers -

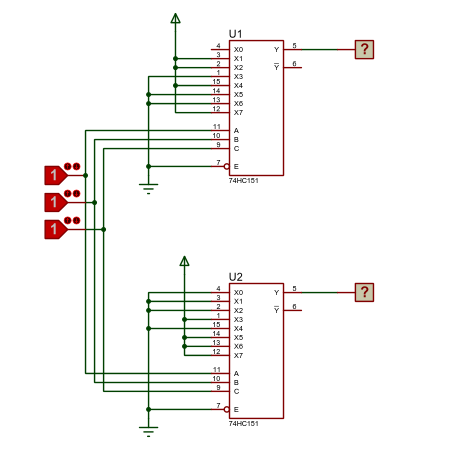
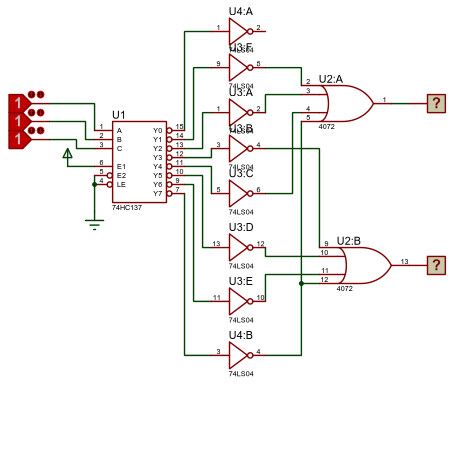
Implementation using Decoder -